Three-Toed Sloth

Return of "Homophily, Contagion, Confounding: Pick Any Three", or, The Adventures of Irene and Joey Along the Back-Door Paths

Attention conservation notice: 2700 words on a new paper on causal inference in social networks, and why it is hard. Instills an attitude of nihilistic skepticism and despair over a technical enterprise you never knew existed, much less cared about, which a few feeble attempts at jokes and a half-hearted constructive suggestion at the end fail to relieve. If any of this matters to you, you can always check back later and see if it survived peer review.

Well, we decided for a more sedate title for the actual paper, as opposed to the talk:

CRS and Andrew C. Thomas, "Homophily and Contagion Are Generically Confounded in Observational Social Network Studies", arxiv:1004.4704, Sociological Methods and Research 40 (2011): 211--239 [citation updated]

Abstract: We consider processes on social networks that can potentially involve three phenomena: homophily, or the formation of social ties due to matching individual traits; social contagion, also known as social influence; and the causal effect of an individual's covariates on their behavior or other measurable responses. We show that, generically, all of these are confounded with each other. Distinguishing them from one another requires strong assumptions on the parametrization of the social process or on the adequacy of the covariates used (or both). In particular we demonstrate, with simple examples, that asymmetries in regression coefficients cannot identify causal effects, and that very simple models of imitation (a form of social contagion) can produce substantial correlations between an individual's enduring traits and their choices, even when there is no intrinsic affinity between them. We also suggest some possible constructive responses to these results.

R code for our simulations

The basic problem here is as follows. (I am afraid this will spoil some of the jokes in the paper.) Consider the venerable parental question: "If your friend Joey jumped off a bridge, would you jump too?" The fact of the matter is that the answer is "yes"; but why does Joey's jumping off a bridge mean that Joey's friend Irene is more likely to jump off one too?

1. Influence or social contagion: Because they are friends, Joey's example inspires Irene to jump. Or, more subtly: seeing Joey jump re-calibrate's Irene's tolerance for risky behavior, which makes jumping seem like a better idea.
2. Biological contagion: Joey is infected with a parasite which suppresses the fear of heights and/or falling, and, because they are friends, Joey passes it on to Irene.
3. Manifest homophily: Joey and Irene are friends because they both like to jump off bridges (hopefully with bungee cords attached).
4. Latent homophily: Joey and Irene are friends because they are both hopeless adrenaline junkies, and met through a roller-coaster club; their common addiction leads both of them to take up bridge-jumping.
5. External causation: Sometimes, jumping off a bridge is the only sane thing to do:

For Irene's parents, there is a big difference between (1) and (2) and the other explanations. The former suggest that it would be a good idea to keep Irene away from Joey, or at least to keep Joey from jumping off the bridge; with the others, however, that's irrelevant. In the case of (3) and (4), in fact, knowing that Irene is friends with Joey is just a clue as to what Irene is really like; the damage was already done, and they can hang out together as much as they want. The difference between these accounts is one of causal mechanisms. (Of course there can be mixed cases.)

What the statistician or social scientist sees is that bridge-jumping is correlated across the social network. In this it resembles many, many, many behaviors and conditions, such as prescribing new antibiotics (one of the classic examples), adopting other new products, adopting political ideologies, attaching tags to pictures on flickr, attaching mis-spelled jokes to pictures of cats, smoking, drinking, using other drugs, suicide, literary tastes, coming down with infectious diseases, becoming obese, and having bad acne or being tall for your age. For almost all of these conditions or behaviors, our data is purely observational, meaning we cannot, for one reason or another, just push Joey off the bridge and see how Irene reacts. Can we nonetheless tell whether bridge-jumping spreads by (some form) of contagion, or rather is due to homophily, or, if it is both, say how much each mechanism contributes?

A lot of people have thought so, and have tried to come at it in the usual way, by doing regression. Most readers can probably guess what I think about that, so I will just say: don't you wish. More sophisticated ideas, like propensity score matching, have also been tried, but people have pretty much assumed that it was possible to do this sort of decomposition. What Andrew and I showed is that in fact it isn't, unless you are willing to make very strong, and generally untestable, assumptions.

This becomes clear as soon as you draw the relevant graphical model, which goes like so:

Here i stands for Irene and j for Joey. Y(i,t) is 1 if Irene jumps off the bridge on day t and 0 otherwise; likewise Y(j,t-1) is whether Joey jumped off the bridge yesterday. We want to know whether the latter variable influences the former. A(i,j) is how we represent the social network --- it's 1 if Irene regards Joey as a friend, 0 otherwise. Lurking in the background are the various traits which might affect whether or not Irene and Joey are friends, and whether or not they like to jump off bridges, collectively X. Suppose that, all else equal, being more similar makes it more likely that people become friends.

Now it's easy to see where the trouble lies. If we learn that Joey jumped off a bridge yesterday, that tells us something about what kind of person Joey is, X(j). If Joey and Irene are friends, that tells us something about what kind of person Irene is, X(i), and so about whether Irene will jump off a bridge today. And this is so whether or not there is any direct influence of Joey's behavior on Irene's, whether or not there is contagion. The chain of inferences — from Joey's behavior to Joey's latent traits, and then over the social link to Irene's traits and thus to Irene's behavior — constitutes what Judea Pearl strikingly called a "back-door path" connecting the variables at either end. When such paths exist, as here, Y(i,t) will be at least somewhat predictable from Y(j,t-1), and sufficiently clever regressions will detect this, but they cannot distinguish how much of the predictability is due to the back door path and how much to direct influence. If this sounds hand-wavy to you, and you suspect that with some fancy adjustments you can duck and weave through it, read the paper.

To switch examples to something a little more serious than jumping off bridges, let's take it as a given that (as Christakis and Fowler famously reported), if Joey became obese last year, the odds of Irene becoming obese this year go up substantially. They interpreted this as a form of social contagion, and one can imagine various influences through which it might work (changing Irene's perception of what normal weight is, changing Irene's perception of what normal food consumption is, changes in happiness leading to changes in comfort food and/or comfort alcohol consumption, etc.). Now suppose that there is some factor X which affects both whether Joey and Irene become friends, and whether and when they become obese. For example:

• becoming friends because they both do extreme sports (like jumping off bridges...) vs. becoming friends because they both really like watching the game on weekends and going through a few six-packs vs. becoming friends because they are both confrontational-spoken-word performance artists;
• friendships tend to be within ethnic groups, which differ in their culturally-transmitted foodways, attitudes towards voluntary exercise, and occupational opportunities;
• (for those more fond of genetic explanations than I am): friendships tend to be within ethnic groups, so friends tend to be more genetically similar than random pairs of individuals, and genetic variants that predispose to obesity (in the environment of Framingham, Mass.) are more common in some groups than in others.

So long as we cannot measure X, the back-door path linking Joey and Irene remains open, and our inferences about contagion are confounded. It would be enough to measure the aspect of X which influences link formation, or the aspect which influences obesity; but without that, there will always be many ways of combining homophily and contagion to produce any given pattern of association between Joey's obesity status last year and Irene's this year. And it's not matter of not being able to decide among some causal alternatives due to limited data; the different causal alternatives all produce the same observable outcomes. (More on this notion of "identification".)

Christakis and Fowler made an interesting suggestion in their obesity paper, however, which was actually one of the most challenging things for us to deal with. They noticed that friendships are sometimes not reciprocated, that Irene thinks of Joey as a friend, but Joey doesn't think of Irene that way — or, more cautiously, Irene reports Joey as a friend, but Joey doesn't name Irene. For these asymmetric pairs in their data, Christakis and Fowler note, it's easier to predict the person who named a friend from the behavior of the nominee than vice versa. This is certainly compatible with contagion, in the form of being influenced by those you regard as your friends, but is there any other way to explain it?

As it happens, yes. One need only suppose that being a certain kind of person — having certain values of the latent trait X — make you more likely to be (or be named as) a friend. Suppose that there is just a one-dimensional trait, like your location on the left-right political axis, or perhaps some scale of tastes. (Perhaps Irene and Joey are neo-conservative intellectuals, and the trait in question is just how violent they like their Norwegian black metal music.) Having similar values of the trait makes you more likely to be friends (that's homophily), but there is always an extra tendency to be friends with those who are closer to the median of the distribution, or at least to say those are who your friends are. (Wherever neo-conservatives really are on the black metal spectrum, they tend to say, on Straussian grounds, that their friends are those who prefer only the median amount of church-burning with their music.) If Irene thinks of Joey as a friend, but Joey does not, this is a sign that Irene has a more extreme value of the trait than Joey does, which changes how much their behavior predicts each other. Putting together a very basic model of this sort shows that it robustly generates the kind of asymmetry Christakis and Fowler found, even when there is really no contagion.

To be short about it, unless you actually know, and appropriately control for, the things which really lead people to form connections, you really have no way of distinguishing between contagion and homophily.

All of this can be turned around, however. Suppose that you want to know whether, or how strongly, some trait of people influences their choices. Following a long tradition with many illustrious exponents, for instance, people are very convinced that social class influences political choices, and there is indeed a predictive relationship here, though many people are totally wrong about what that relationship is. The natural supposition is that this predictive relationship reflects causation. But suppose that there is contagion, that you can catch ideology or even just choices from your friends. Social class is definitely a homophilous trait; this means that an opinion or attitude or choice can become entrenched among one social class, and not another, simply through diffusion, even if there is no intrinsic connection between them. And there's nothing special about class here; it could be any trait or combination of traits which leads to homophily.

Here, for example, is a simple simulation done using Andrew's ElectroGraph package.

To explain: Each individual has a social type or trait, which takes one of two values and stays fixed — think of this as social class, if you like. People are more likely to form links with those of the same type, so when we plot the graph in a way which brings linked nodes closer to each other, we get a nice separation into two sub-communities, with all the upper-class individuals in the one on top and all the lower-class individuals in the one below. Also, each individual makes a "choice" which can change over time, which again is binary, here "red" or "blue". Initially, choices are completely independent of traits, so there's just as much red among the high-class individuals as among the low.

Now let the choices evolve according to the simplest possible rule: at each point in time, a random individual picks one of their neighbors, again at random, and copies their opinion. After a few hundred such updates, the lower class has turned red, and the upper class has turned blue:

And this isn't just a fluke; the pattern of color separation repeats quite reliably, though which color goes with which class is random. If you wanted to be more quantitative about it, you could, say, run a logistic regression, and discovery that in the homophilous network, statistically-significant prediction of choice from trait is possible, but not in an otherwise-matched network without homophily; you can see those results in the paper. A bit more abstractly, when I learned cellular automata from David Griffeath, one of the topics was something called the "voter model", which is just the rule I gave above for copying choices. On a regular two-dimensional grid, the voter model self-organizes from random noise into blobs of homogeneous color with smooth boundaries; this is just the corresponding behavior on a graph. As I have said several times before, I think this phenomenon — correlating traits and choices by homophily plus contagion — seriously complicates a lot of what people want to do in the social sciences and even the humanities, but since I have gone on about that already, I won't re-rant today.

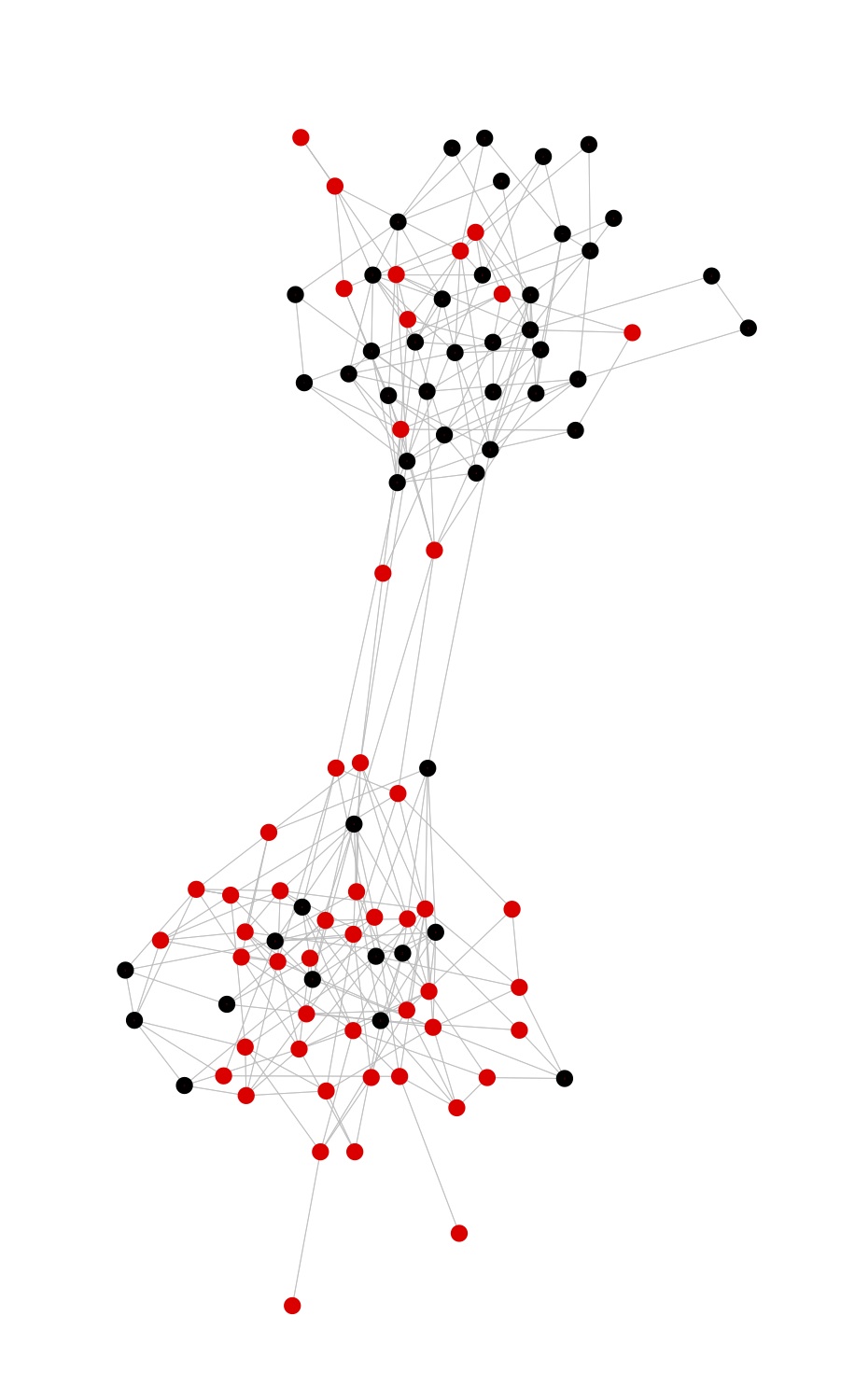
In their own way, each of the two models in our paper is sheer elegance in its simplicity, and I have been known to question the relevance of such models for actual social science. I don't think I'm guilty of violating my own strictures, however, because I'm not saying that the processes of, say, spreading political opinions really follows a voter model. (The reality is much more complicated.) The models make vivid what was already proved, and show that the conditions needed to produce the phenomena are not actually very extreme.

My motto as a writer might as well be "the urge to destroy is also a creative urge", but in this paper we do hold out some hope, which is that even if the causal effects of contagion and/or homophily cannot be identified, they might be bounded, following the approach pioneered by Manski for other unidentifiable quantities. Even if observable associations would never let us say exactly how strong contagion is, for instance, they might let us say that it has to lie inside some range, and if that range excludes zero, we know that contagion must be at work. (Or, if the association is stronger than contagion can produce, something else must be at work.) I suspect (with no proof) that one way to get useful bounds would be to use the pattern of ties in the network to divide it into sub-networks or, as we say in the trade, communities, and use the estimated communities as proxies for the homophilous trait. That is, if people tend to become friends because they are similar to each other, then the social network will tend to become a set of clumps of similar people, as in the figures above. So rather than just looking at the tie between Joey and Irene, we look at who else they are friends with, and who their friends are friends with, and so on, until we figure out how the network is divided into communities and that (say) Irene and Joey are in the same community, and therefore likely have the similar values of X, whatever it is. Adjusting for community might then approach actually adjusting for X, though it couldn't be quite the same. Right now, though, this idea is just a conjecture we're pursuing.

Manual trackback: The Monkey Cage; Citation Needed; Healthy Algorithms; Siris; Gravity's Rainbow; Orgtheory; PeteSearch; A Fine Theorem

Update, 11 July 2011: further developments!

Networks; Enigmas of Chance; Complexity; Commit a Social Science; Self-Centered